Онлайн калькулятор надёжности. расчёт надёжности онлайн

Интенсивность отказов

Интенсивностью отказов λ(t) называется отношение числа отказавших объектов в единицу времени к среднему числу объектов, работающих в данный отрезок времени, при условии, что отказавшие объекты не восстанавливаются и не заменяются исправными: λ(t) = n(t)/[N_срΔt] где N_ср = [N_i + N_i+1]/2 — среднее число объектов, исправно работавших в интервале времени Δt; N_i – число изделий, работавших в начале интервала Δt; N_i+1 – число объектов, исправно работавших в конце интервала времени Δt.

Ресурсные испытания и наблюдения над большими выборками объектов показывают, что в большинстве случаев интенсивность отказов изменяется во времени немонотонно.

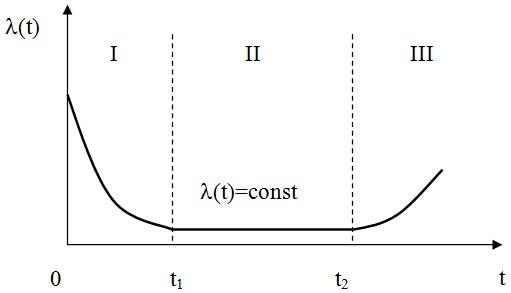Типичная кривая изменения интенсивности отказов объекта

Из кривой зависимости отказов от времени видно, что весь период работы объекта можно условно поделить на 3 периода. I — й период – приработка.

Приработочные отказы являются, как правило, результатом наличия у объекта дефектов и дефектных элементов, надежность которых значительно ниже требуемого уровня. При увеличении числа элементов в изделии даже при самом строгом контроле не удается полностью исключить возможность попадания в сборку элементов, имеющих те или иные скрытые дефекты. Кроме того, к отказам в этот период могут приводить и ошибки при сборке и монтаже, а также недостаточная освоенность объекта обслуживающим персоналом.

Физическая природа таких отказов носит случайный характер и отличается от внезапных отказов нормального периода эксплуатации тем, что здесь отказы могут иметь место не при повышенных, а и при незначительных нагрузках («выжигание дефектных элементов»). Снижение величины интенсивности отказов объекта в целом, при постоянном значении этого параметра для каждого из элементов в отдельности, как раз и объясняется «выжиганием» слабых звеньев и их заменой наиболее надежными. Чем круче кривая на этом участке, тем лучше: меньше дефектных элементов останется в изделии за короткий срок.

Чтобы повысить надежность объекта, учитывая возможность приработочных отказов, нужно: • проводить более строгую отбраковку элементов; • проводить испытания объекта на режимах близких к эксплуатационным и использовать при сборке только элементы, прошедшие испытания; • повысить качество сборки и монтажа.

Среднее время приработки определяют при испытаниях. Для особо важных случаев необходимо увеличить срок приработки в несколько раз по сравнению со средним.

II — й период – нормальная эксплуатация Этот период характеризуется тем, что приработочные отказы уже закончились, а отказы, связанные с износом, еще не наступили. Этот период характеризуется исключительно внезапными отказами нормальных элементов, наработка на отказ которых очень велика.

Сохранение уровня интенсивности отказов на этом этапе характеризуется тем, что отказавший элемент заменяется таким же, с той же вероятностью отказа, а не лучшим, как это происходило на этапе приработки.

Отбраковка и предварительная обкатка элементов, идущих на замену отказавших, имеет для этого этапа еще большее значение. Наибольшими возможностями в решении этой задачи обладает конструктор. Нередко изменение конструкции или облегчение режимов работы всего одного-двух элементов обеспечивает резкое повышение надежности всего объекта. Второй путь – повышение качества производства и даже чистоты производства и эксплуатации.

III – й период – износ Период нормальной эксплуатации заканчивается, когда начинают возникать износовые отказы. Наступает третий период в жизни изделия – период износа.

Вероятность возникновения отказов из-за износов с приближением к сроку службы возрастает.

С вероятностной точки зрения отказ системы в данном промежутке времени Δt = t₂ – t₁ определяется как вероятность отказа:

∫a(t) = Q₂(t) — Q₁(t)

Интенсивность отказов есть условная вероятность того, что в промежуток времени Δt произойдет отказ при условии, что до этого он не произошел λ(t) = [Q₂ — Q₁]/ λ(t) = lim [Q₂ — Q₁]/ = / = Q'(t)/P(t) = -P'(t)/P(t) так как a(t) = -P'(t), то λ(t) = a(t)/P(t).

Эти выражения устанавливают зависимость между вероятностью безотказной работы, частотой и интенсивностью отказов. Если a(t) – невозрастающая функция, то справедливо соотношение: ω(t) ≥ λ(t) ≥ a(t).

Методы расчёта надёжности

Структурные методы расчета надёжности

Структурные методы являются основными методами расчета показателей надёжности в процессе проектирования объектов, поддающихся разукрупнению на элементы, характеристики надёжности, которых в момент проведения расчетов известны или могут быть определены другими методами.
Расчет показателей надёжности структурными методами в общем случае включает:

• представление объекта в виде структурной схемы, описывающей логические соотношения между состояниями элементов и объекта в целом с учетом структурно-функциональных связей и взаимодействия элементов, принятой стратегии обслуживания, видов и способов резервирования и других факторов;
• описание построенной структурной схемы надёжности объекта адекватной математической моделью, позволяющей в рамках введенных предположений и допущений вычислить показатели надёжности объекта по данным о надёжности его элементов в рассматриваемых условиях применения.

В качестве структурных схем надёжности могут применяться:

• схемы функциональной целостности;
• структурные блок-схемы надёжности;
• деревья отказов;
• графы состояний и переходов.

Логико-вероятностный метод

В логико-вероятностных методах (ЛВМ) исходная постановка задачи и построение модели функционирования исследуемого системного объекта или процесса осуществляется структурными и аналитическими средствами математической логики, а расчет показателей свойств надёжности, живучести и безопасности выполняется средствами теории вероятностей.

ЛВМ являются методологией анализа структурно-сложных систем, решения системных задач организованной сложности, оценки и анализа надёжности, безопасности и риска технических систем. ЛВМ удобны для исходной формализованной постановки задач в форме структурного описания исследуемых свойств функционирования сложных и высокоразмерных систем. В ЛВМ разработаны процедуры преобразования исходных структурных моделей в искомые расчетные математические модели, что позволяет выполнить их алгоритмизацию и реализацию на ЭВМ.

Основоположником научно-технического аппарата ЛВМ и прикладных аспектов их применения, а также создателем и руководителем научной школы является профессор Рябинин И. А..

Общий логико-вероятностный метод

Необходимость распространения ЛВМ на немонотонные процессы привела к созданию общего логико-вероятностного метода (ОЛВМ). В ОЛВМ расчета надёжности аппарат математической логики используется для первичного графического и аналитического описания условий реализации функций отдельными и группами элементов в проектируемой системе, а методы теории вероятностей и комбинаторики применяются для количественной оценки безотказности и/или опасности функционирования проектируемой системы в целом. Для использования ОЛВМ должны задаваться специальные структурные схемы функциональной целостности исследуемых систем, логические критерии их функционирования, вероятностные и другие параметры элементов.

В основе постановки и решения всех задач моделирования и расчета надёжности систем с помощью ОЛВМ лежит так называемый событийно-логический подход. Этот подход предусматривает последовательное выполнение следующих четырёх основных этапов ОЛВМ:

• этап структурно-логической постановки задачи;
• этап логического моделирования;
• этап вероятностного моделирования;
• этап выполнения расчетов показателей надёжности.

Цели расчета надёжности

Решение вопросов надёжности и безопасности современных структурно-сложных технических систем и объектов осуществляется на всех стадиях жизненного цикла, от проектирования и создания, производства, до эксплуатации, использования и утилизации. При этом могут преследоваться следующие цели:

• обоснование количественных требований к надёжности объекта или его составным частям;
• сравнительный анализ надёжности вариантов схемно-конструктивного построения объекта и обоснование выбора рационального варианта, в том числе по стоимостному критерию;
• определение достигнутого (ожидаемого) уровня надёжности объекта и/или его составных частей, в том числе расчетное определение показателей надёжности или параметров распределения характеристик надежности составных частей объекта в качестве исходных данных для расчета надёжности объекта в целом;
• обоснование и проверку эффективности предлагаемых (реализованных) мер по доработкам конструкции, технологии изготовления, системы технического обслуживания и ремонта объекта, направленных на повышение его надёжности;
• решение различных оптимизационных задач, в которых показатели надёжности выступают в роли целевых функций, управляемых параметров или граничных условий, в том числе таких, как оптимизация структуры объекта, распределение требований по надёжности между показателями отдельных составляющих надёжности (например, безотказности и ремонтопригодности), расчет комплектов ЗИП, оптимизация систем технического обслуживания и ремонта, обоснование гарантийных сроков и назначенных сроков службы (ресурса) объекта и др.;
• проверку соответствия ожидаемого (достигнутого) уровня надёжности объекта установленным требованиям (контроль надежности), если прямое экспериментальное подтверждение их уровня надёжности невозможно технически или нецелесообразно экономически.

На этапе проектирования технических систем выполняется проектный расчет надёжности.

Проектный расчет надёжности — процедура определения значений показателей надёжности объекта на этапе проектирования с использованием методов, основанных на их вычислении по справочным и другим данным о надёжности элементов объекта, имеющихся к моменту расчета.

Проектный расчет надёжности входит в состав обязательных работ по обеспечению надёжности любой автоматизированной системы и выполняется на основе требований нормативно-технической документации (ГОСТ 27.002-89, ГОСТ 27.301-95, ГОСТ 24.701-86).

На этапе испытаний и эксплуатации расчёт надёжности проводится для оценки количественных показателей надёжности спроектированной системы.

Типичные распределения времени безотказной работы

• Экспоненциальное распределение: f(t)=λe−λt{\displaystyle f(t)=\lambda e^{-\lambda t}}, λ>{\displaystyle \lambda >0}, t⩾{\displaystyle t\geqslant 0}.
• Гамма-распределение: f(t)=λ(λt)α−1e−λtΓ(α){\displaystyle f(t)={\frac {\lambda (\lambda t)^{\alpha -1}e^{-\lambda t}}{\Gamma (\alpha )}}}, λ,α>{\displaystyle \lambda ,\alpha >0}, t⩾{\displaystyle t\geqslant 0}.
• Распределение Вейбулла: f(t)=λαtα−1e−λtα{\displaystyle f(t)=\lambda \alpha t^{\alpha -1}e^{-\lambda t^{\alpha }}}, λ,α>{\displaystyle \lambda ,\alpha >0}, t⩾{\displaystyle t\geqslant 0}.
• Модифицированное распределение экстремального значения: f(t)=1λexp⁡−et−1λ+t{\displaystyle f(t)={\frac {1}{\lambda }}\exp {\left}}, λ>{\displaystyle \lambda >0}, t⩾{\displaystyle t\geqslant 0}.
• Усечённое нормальное распределение: f(t)=1aσ2πexp⁡−(t−μ)22σ2{\displaystyle f(t)={\frac {1}{a\sigma {\sqrt {2\pi }}}}\exp {\left}}, σ>{\displaystyle \sigma >0}, −∞<μ<∞{\displaystyle -\infty <\mu <\infty }, <t<∞{\displaystyle 0<t<\infty }.
• Логарифмически-нормальное распределение: f(t)=1tσ2πexp⁡−(lg⁡t−μ)22σ2{\displaystyle f(t)={\frac {1}{t\sigma {\sqrt {2\pi }}}}\exp {\left}}, σ>{\displaystyle \sigma >0}, −∞<μ<∞{\displaystyle -\infty <\mu <\infty }, t⩾{\displaystyle t\geqslant 0}.

Интенсивность отказов неэлектронных компонентов

Если интересует интенсивность отказов неэлектронных компонентов, лучшим решением будет посмотреть справочник NRPD-91 (non-electronic reliability part data). Потребуется знание английского языка. Есть и более свежие версии этого справочника, но их продают за неприличные деньги.

Скачать NRPD-91 можно здесь. 39 мегабайт.

Нетрудно заметить, что чем меньше время работы оборудования, тем оно надёжнее. Это доступный, но не всегда выполнимый способ повысить надёжность системы — сократить время работы. Приведу простой пример: многие люди стирая одежду в стиральной машине используют полную программу стирки, которая занимает, предположим, 2 часа работы.

Давайте рассчитаем надёжность (ВБР) электродвигателя нашей стиралки. По таблице ниже найдём λ для электродвигателя переменного тока. Выберем наихудшее значение: 9.36 Предположим, что мы стираем 200 дней в году на протяжении 5 лет. Тогда время работы составит: 200 дней * 2 часа в день * 5 лет = 2000 часов за 5 лет. Подставим в нашу формулу (1). ВБР электродвигателя составит 0.9814.

А если мы хотим, чтобы наша стиралка служила нам дольше? В действительности, в большинстве случаев нет необходимости стирать наши рубашки 2 часа, получаса (0.5 часа) будет вполне достаточно. Давайте рассчитаем ВБР электродвигателя в этом случае. Время работы составит: 200 дней * 0.5 часа * 5 лет = 500 часов за 5 лет. Подставим в нашу формулу (1). ВБР электродвигателя составит 0.9953. Как видим, надёжность электродвигателя стала выше.

Интенсивность отказов сердца

Вот бы таким же образом можно было продлить жизнь человека, скажет читатель. Это вполне возможно. Чем ниже наш пульс, тем меньше ударов совершает наше сердце и тем меньше оно изнашивается. Вспомните, один из самых завидных долгожителей нашей планеты это черепаха, пульс которой гораздо меньше чем человеческий. Конечно, мы не можем себе позволить быть такими же медлительными.

Кто-то даже подсчитал, что ресурс человеческого сердца это 3 миллиарда ударов и определил интенсивность отказов сердца. Не уверен, что это правда, но зато абсолютно уверен, что мы вполне можем отказаться от курения, больших доз алкоголя, кофеина, энергетиков, чрезмерных физических нагрузок, стрессов на пустом месте и подобных вещей, которые разгоняют наш пульс и съедают ресурс нашего сердца. Напротив, умеренная физическая нагрузка тренирует наше сердце и продляет нашу жизнь. Будьте здоровы и счастливы! Ваш специалист по надёжности, Алексей Глазачев.

Если вы хотите мгновенно делать сложнейший расчет надежности и экономить десятки часов рабочего времени, приглашаю вас получить мой пример расчета надежности в Excel.