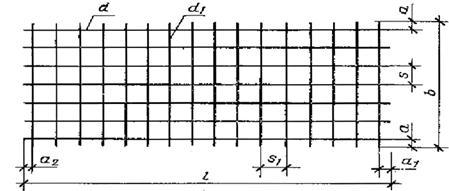
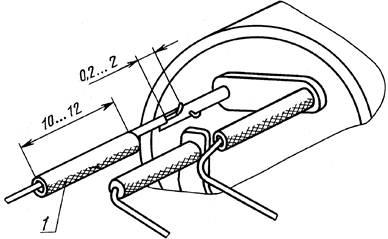
Гост 5781-82 сталь горячекатаная для армирования железобетонных конструкций. технические условия (с изменениями n 1, 2, 3, 4, 5)
Содержание:
Заземление и зануление
5.4.56. Заземление и зануление должны быть выполнены в соответствии с требованиями гл. 1.7. Считается достаточным, если части, подлежащие заземлению или занулению, присоединены к металлическим конструкциям крана, при этом должна быть обеспечена непрерывность электрической цепи металлических конструкций. Если электрооборудование крана установлено на его заземленных металлических конструкциях и на опорных поверхностях предусмотрены зачищенные и незакрашенные места для обеспечения электрического контакта, то дополнительного заземления не требуется.
Рельсы кранового пути должны быть надежно соединены на стыках (сваркой, приваркой перемычек достаточного сечения, приваркой к металлическим подкрановым балкам) одна с другой для создания непрерывной электрической цепи. В электроустановках, для которых в качестве защитного мероприятия применяется заземление или зануление, рельсы кранового пути должны быть соответственно заземлены или занулены.
При установке крана на открытом воздухе рельсы кранового пути, кроме того, должны быть соединены между собой и заземлены, при этом для заземления рельсов необходимо предусматривать не менее двух заземлителей, присоединяемых к рельсам в разных местах.
5.4.57. При питании крана кабелем должны быть выполнены кроме требования 5.4.56 также требования гл. 1.7, предъявляемые к передвижным электроустановкам.
5.4.58. Корпус кнопочного аппарата управления крана, управляемого с пола, должен быть выполнен из изоляционного материала или заземлен (занулен) не менее чем двумя проводниками. В качестве одного из проводников может быть использован тросик, на котором подвешен кнопочный аппарат.
Зануление и заземление
7.3.132. На взрывоопасные зоны любого класса в помещениях и на наружные взрывоопасные установки распространяются приведенные в 1.7.38 требования о допустимости применения в электроустановках до 1 кВ глухозаземленной или изолированной нейтрали. При изолированной нейтрали должен быть обеспечен автоматический контроль изоляции сети с действием на сигнал и контроль исправности пробивного предохранителя.
7.3.133. Во взрывоопасных зонах классов B-I, B-Iа и B-II рекомендуется применять защитное отключение (см. гл. 1.7). Во взрывоопасных зонах любого класса должно быть выполнено уравнивание потенциалов согласно 1.7.47.
7.3.134. Во взрывоопасных зонах любого класса подлежат занулению (заземлению) также:
а) во изменение 1.7.33 — электроустановки при всех напряжениях переменного и постоянного тока;
б) электрооборудование, установленное на зануленных (заземленных) металлических конструкциях, которые в соответствии с 1.7.48, п. 1 в невзрывоопасных зонах разрешается не занулять (не заземлять). Это требование не относится к электрооборудованию, установленному внутри зануленных (заземленных) корпусов шкафов и пультов.
В качестве нулевых защитных (заземляющих) проводников должны быть использованы проводники, специально предназначенные для этой цели.
7.3.135. В электроустановках до 1 кВ с глухозаземленной нейтралью зануление электрооборудования должно осуществляться:
а) в силовых сетях во взрывоопасных зонах любого класса отдельной жилой кабеля или провода;
б) в осветительных сетях во взрывоопасных зонах любого класса, кроме класса B-I, — на участке от светильника до ближайшей ответвительной коробки — отдельным проводником, присоединенным к нулевому рабочему проводнику в ответвительной коробке;
в) в осветительных сетях во взрывоопасной зоне класса B-I — отдельным проводником, проложенным от светильника до ближайшего группового щитка;
г) на участке сети от РУ и ТП, находящихся вне взрывоопасной зоны, до щита, сборки, распределительного пункта и т. п., также находящихся вне взрывоопасной зоны, от которых осуществляется питание электроприемников, расположенных во взрывоопасных зонах любого класса, допускается в качестве нулевого защитного проводника использовать алюминиевую оболочку питающих кабелей.
7.3.136. Нулевые защитные проводники во всех звеньях сети должны быть проложены в общих оболочках, трубах, коробах, пучках с фазными проводниками.
7.3.137. В электроустановках до 1 кВ и выше с изолированной нейтралью заземляющие проводники допускается прокладывать как в общей оболочке с фазными, так и отдельно от них.
Магистрали заземления должны быть присоединены к заземлителям в двух или более разных местах и по возможности с противоположных концов помещения.
7.3.138. Использование металлических конструкций зданий, конструкций производственного назначения, стальных труб электропроводки, металлических оболочек кабелей и т. п. в качестве нулевых защитных (заземляющих) проводников допускается только как дополнительное мероприятие.
7.3.139. В электроустановках до 1 кВ с глухозаземленной нейтралью в целях обеспечения автоматического отключения аварийного участка проводимость нулевых защитных проводников должна быть выбрана такой, чтобы при замыкании на корпус или нулевой защитный проводник возникал ток КЗ, превышающий не менее чем в 4 раза номинальный ток плавкой вставки ближайшего предохранителя и не менее чем в 6 раз ток расцепителя автоматического выключателя, имеющего обратнозависимую от тока характеристику.
При защите сетей автоматическими выключателями, имеющими только электромагнитный расцепитель (без выдержки времени), следует руководствоваться требованиями, касающимися кратности тока КЗ и приведенными в 1.7.79.
7.3.140. Расчетная проверка полного сопротивления петли фаза-нуль в электроустановках напряжением до 1 кВ с глухозаземленной нейтралью должна предусматриваться для всех электроприемников, расположенных во взрывоопасных зонах классов B-I и B-II, и выборочно (но не менее 10% общего количества) для электроприемников, расположенных во взрывоопасных зонах классов B-Iа, B-Iб, B-Iг и ВIIа и имеющих наибольшее сопротивление петли фаза-нуль.
7.3.141. Проходы специально проложенных нулевых защитных (заземляющих) проводников через стены помещений со взрывоопасными зонами должны производиться в отрезках труб или в проемах. Отверстия труб и проемов должны быть уплотнены несгораемыми материалами. Соединение нулевых защитных (заземляющих) проводников в местах проходов не допускается.
Перевод чисел из десятичной системы счисления в другую систему счисления
Для перевода чисел из десятичной системы счисления в другую систему счисления нужно переводить отдельно целую часть числа и дробную часть числа.
Целую часть числа переводится из десятичной СС в другую систему счисления — последовательным делением целой части числа на основание системы счисления (для двоичной СС — на 2, для 8-ичной СС — на 8, для 16-ичной — на 16 и т.д.) до получения целого остатка, меньше, чем основание СС.
Пример 4. Переведем число 159 из десятичной СС в двоичную СС:
| 159 | 2 | ||||||
| 158 | 79 | 2 | |||||
| 1 | 78 | 39 | 2 | ||||
| 1 | 38 | 19 | 2 | ||||
| 1 | 18 | 9 | 2 | ||||
| 1 | 8 | 4 | 2 | ||||
| 1 | 4 | 2 | 2 | ||||
| 2 | 1 |
Рис. 1
Как видно из Рис. 1, число 159 при делении на 2 дает частное 79 и остаток 1. Далее число 79 при делении на 2 дает частное 39 и остаток 1 и т.д. В результате построив число из остатков деления (справа налево) получим число в двоичной СС: 10011111. Следовательно можно записать:
Пример 5. Переведем число 615 из десятичной СС в восьмеричную СС.
| 615 | 8 | ||
| 608 | 76 | 8 | |
| 7 | 72 | 9 | 8 |
| 4 | 8 | 1 | |
| 1 |
Рис. 2
При приведении числа из десятичной СС в восьмеричную СС, нужно последовательно делить число на 8, пока не получится целый остаток меньшее, чем 8. В результате построив число из остатков деления (справа налево) получим число в восьмеричной СС: 1147(см. Рис. 2). Следовательно можно записать:
Пример 6. Переведем число 19673 из десятичной системы счисления в шестнадцатеричную СС.
| 19673 | 16 | ||
| 19664 | 1229 | 16 | |
| 9 | 1216 | 76 | 16 |
| 13 | 64 | 4 | |
| 12 |
Рис. 3
Как видно из рисунка Рис.3, последовательным делением числа 19673 на 16 получили остатки 4, 12, 13, 9. В шестнадцатеричной системе счисления числе 12 соответствует С, числе 13 — D. Следовательно наше шестнадцатеричное число — это 4CD9.
Далее рассмотрим перевод правильных десятичных дробей в двоичную СС, в восьмеричную СС, в шестнадцатеричную СС и т.д.
Для перевода правильных десятичных дробей (вещественное число с нулевой целой частью) в систему счисления с основанием s необходимо данное число последовательно умножить на s до тех пор, пока в дробной части не получится чистый нуль, или же не получим требуемое количество разрядов. Если при умножении получится число с целой частью, отличное от нуля, то эту целую часть не учитывать (они последовательно зачисливаются в результат).
Рассмотрим вышеизложенное на примерах.
Пример 7. Переведем число 0.214 из десятичной системы счисления в двоичную СС.
| 0.214 | ||
| x | 2 | |
| 0.428 | ||
| x | 2 | |
| 0.856 | ||
| x | 2 | |
| 1 | 0.712 | |
| x | 2 | |
| 1 | 0.424 | |
| x | 2 | |
| 0.848 | ||
| x | 2 | |
| 1 | 0.696 | |
| x | 2 | |
| 1 | 0.392 |
Рис. 4
Как видно из Рис.4, число 0.214 последовательно умножается на 2. Если в результате умножения получится число с целой частью, отличное от нуля, то целая часть записывается отдельно (слева от числа), а число записывается с нулевой целой частью. Если же при умножении получиться число с нулевой целой частью, то слева от нее записывается нуль. Процесс умножения продолжается до тех пор, пока в дробной части не получится чистый нуль или же не получим требуемое количество разрядов. Записывая жирные числа (Рис.4) сверху вниз получим требуемое число в двоичной системе счисления: 0.0011011.
Следовательно можно записать:
Пример 8. Переведем число 0.125 из десятичной системы счисления в двоичную СС.
| 0.125 | ||
| x | 2 | |
| 0.25 | ||
| x | 2 | |
| 0.5 | ||
| x | 2 | |
| 1 | 0.0 |
Рис. 5
Для приведения числа 0.125 из десятичной СС в двоичную, данное число последовательно умножается на 2. В третьем этапе получилось 0. Следовательно, получился следующий результат:
Пример 9. Переведем число 0.214 из десятичной системы счисления в шестнадцатеричную СС.
| 0.214 | ||
| x | 16 | |
| 3 | 0.424 | |
| x | 16 | |
| 6 | 0.784 | |
| x | 16 | |
| 12 | 0.544 | |
| x | 16 | |
| 8 | 0.704 | |
| x | 16 | |
| 11 | 0.264 | |
| x | 16 | |
| 4 | 0.224 |
Рис. 6
Следуя примерам 4 и 5 получаем числа 3, 6, 12, 8, 11, 4. Но в шестнадцатеричной СС числам 12 и 11 соответствуют числа C и B. Следовательно имеем:
Пример 10. Переведем число 0.512 из десятичной системы счисления в восьмеричную СС.
| 0.512 | ||
| x | 8 | |
| 4 | 0.096 | |
| x | 8 | |
| 0.768 | ||
| x | 8 | |
| 6 | 0.144 | |
| x | 8 | |
| 1 | 0.152 | |
| x | 8 | |
| 1 | 0.216 | |
| x | 8 | |
| 1 | 0.728 |
Рис. 7
Получили:
Пример 11. Переведем число 159.125 из десятичной системы счисления в двоичную СС. Для этого переведем отдельно целую часть числа (Пример 4) и дробную часть числа (Пример 8). Далее объединяя эти результаты получим:
Пример 12. Переведем число 19673.214 из десятичной системы счисления в шестнадцатеричную СС. Для этого переведем отдельно целую часть числа (Пример 6) и дробную часть числа (Пример 9). Далее объединяя эти результаты получим:
Числа от 1 до 1000 Итоговое повторение всего изученного Арифметические действия Умножение и делениеОтветы к стр. 93
10. Объясни, как можно узнать:
1) один из двух множителей, если известны произведение и другой множитель;
2) делимое, если известны делитель и частное;
3) делитель, если известны делимое и частное.
1) Разделить произведение на известный множитель
2) Умножить частное на делитель
3) Разделить делимое на частное
11. Заполни таблицы.
| Множитель | 23 | 19 | 18 | Делимое | 92 | 168 | 100 | |
| Множитель | 4 | 6 | 4 | Делитель | 2 | 8 | 25 | |
| Произведение | 92 | 114 | 72 | Частное | 46 | 21 | 4 |
12. Реши следующие уравнения.х • 19 = 76 32 • х = 128 560 : х = 8 х : 14 = 6
x • 19 = 76 32 • x = 128x = 76 19 x = 128 32x = 4 x = 4
560 x = 8 x 14 = 6x = 560 8 x = 14 • 6x = 70 x = 84
13. Объясни, что означают записи на полях, и реши уравнения.1) 0 • х = 0 2) b • 0 = 0 3) 0 : с = 0х • 57 = 0 12 : х = 12 х • 14 = 14
789 • х = 0 х : 697 = 0 45 : х = 1
1) и 2) — если один из множителей равен нулю, то произведение равно нулю.
3) — если ноль разделить на любое число, не равное нулю, то получится ноль.
x • 57 = 0 12 x = 12x = 0 57 x = 12 12x = 0 x = 1
x • 14 = 14 789 • x = 0x = 14 14 x = 0 789x = 1 x = 0
x 697 = 0 45 x = 1x = 0 • 697 x = 45 1x = 0 x = 45
14. Вычисли значения выражений.278 • 0 0 : 47 75 • 4 • 0 • 3
278 • 1 94 : 1 36 • (63 — 63) • 10
278 • 0 = 0
278 • 1 = 278
0 47 = 0
94 1 = 94
75 • 4 • 0 • 3 = 0
36 • (63 – 63) • 10 = 36 • 0 • 10 = 0
15. Какие свойства умножения ты знаешь (с. 120)?
Объясни, почему верны следующие равенства:
12 • 35 = 35 • 12 17 • 5 • 2 = 17 • 10
От перестановки множителей произведение не меняется.
Два соседних множителя можно заменить их произведением.
12 • 35 = 35 • 12 — верно на основании переместительного свойства умножения.
17 • 5 • 2 = 17 • 10 — верно на основании того, что два соседних множителя можно заменить их произведением.
16. Покажи на примерах, как можно умножить сумму нескольких чисел на какое-либо число; как можно разделить сумму на число.
(4 + 3) • 2 = 4 • 2 + 3 • 2 = 8 + 6 = 14
(20 + 15) 5 = 20 5 + 15 5 = 4 + 3 = 7
17. Выполни вычисления и проверь их.
4078 • 6 73648 : 8 792 • 300 51200 : 80
8 • 5930 27420 : 6 7800 • 40 34720 : 70
×4078 Проверка: _ 24468|6 6 24 |407824468 _46 42 _48 48
×5930 Проверка: _ 47440|8 8 40 |593047440 _74 72 _24 24
_ 73648|8 Проверка: 72 |9206 ×9206 _16 8 16 73648 _48 48
_ 27420|6 Проверка: 24 |4570 ×4570 _34 6 30 27420 _42 42
×492 Проверка: _ 147600|300 300 120 |492147600 _276 270 _600 600
×7800 Проверка: _ 31200|40 40 280 |7800312000 _320 320
_ 51200|80 Проверка: 48 |640 ×640 _32 80 3251200
_ 34720|70 Проверка: 280 |496 ×496 _672 70 630 34720 _420 420
18. Выполни деление с остатком и сделай проверку.
11978 : 52 34051 : 420 22700 : 74
_ 11978|52 Проверка: 104 |230 ×230 _157 52 156 + 46 18 — ост. 115 11960 11960 + 18 = 11978
_ 34051|420 Проверка: 3360 |81 ×420 _451 81 420 + 42 31 — ост. 336 34020 34020 + 31 = 34051
_ 22700|74 Проверка: 222 |306 ×306 _500 74 444 + 1224 56 — ост. 2142 22644 22644 + 56 = 22700
19. Выложи такую фигуру из палочек. Убери 3 палочки так, чтобы осталось 3 треугольника.
| ← Предыдущая | Следующая → |