Гост р исо 7870-3-2013 статистические методы. контрольные карты. часть 3. приемочные контрольные карты

3.1. Введение в контрольные карты с памятью

При использовании контрольных карт Шухарта решение о
переналадке производственного процесса принимается на основании анализа текущей
выборки. Карты Шухарта называются еще контрольными картами без памяти

При
выборочном контроле в контрольных картах с памятью принимаются во
внимание результаты контроля предыдущих выборок. Такие контрольные карты могут
быть более чувствительными к возмущениям, то есть уже при самом начале сдвига
уровня настройки или изменения технологического рассеяния указывать на
необходимость вмешательства в процесс

В картах Шухарта в качестве контрольной величины
используется некоторая статистика (функция) от текущей выборки , в
качестве которой могут быть, например, выборочное среднее или выборочное
стандартное отклонение. В контрольных картах с памятью наряду с результатами
текущего контроля учитываются результаты контроля на предыдущих выборках. Если
контрольная величина учитывает результаты контроля во всех предыдущих выборках,
то соответствующая контрольная карта обладает неограниченной памятью. Если
используются результаты контроля только по последним  выборкам, то
карта имеет конечную память. При  – карты без памяти.

Различают карты с равномерной и неравномерной
памятью. В первом случае величины из разных этапов контроля в контрольной
величине имеют одинаковый вес, во втором – различный. В картах второго типа
значимость результатов контроля, как правило, уменьшается с удалением от
настоящего момента времени : карты с убывающей памятью.

Для различения выборочных характеристик из разных
выборок вводится индекс времени , принимающий значения от 1 до :  –
момент взятия первой выборки,  – последней. Все взятые до момента
времени  выборки образуют систему
выборочных векторов

, .

Для каждого выборочного вектора по единому правилу
строится статистика . Система выборочных характеристик , , …,  преобразуется
в скалярную контрольную величину . Наиболее простой является
линейная комбинация

.                                                            
(58)

Вид
памяти зависит от коэффициентов  в (110).

В картах Шухарта:

,                                                                            (59)

 ,                                                                                  
(60)

                                             
      (61)

В MOSUM-картах

,                                                                
(62)

 ,                                                                                  
(63)

                             
(64)

Контрольной величиной является скользящее среднее  последних
выборок (mosum= movingsum). Карты имеют конечную и
равномерную память за  периодов.

В EWMA-картах
используют контрольную величину

,    ,                                
(65)

причем
 задается
как требуемое значение уровня настройки процесса или технологического рассеяния.
Контрольная величина является экспоненциально взвешенным средним значением (EWMA=exponentialweightedmovingaverage)
всех выборочных характеристик, полученных к моменту времени . При
последовательной подстановке получаем:

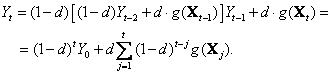                              (66)

Таким образом,

,                                                                     
(67)

,     .            
                                      (68)

Эти карты имеют неограниченную неравномерную память.

В KUSUM-картах
используется контрольная величина:

,                                    
(69)

причем
 задается
как требуемое значение уровня настройки процесса или технологического
рассеяния.

Таким образом,

,                                                                     
(70)

,     .                                                         
(71)

Контрольную величину (69) можно интерпретировать как
накопленную сумму отклонений всех выборочных характеристик от заданного
значения . KUSUM-карты
имеют равномерную память, которая начинается с момента времени .

[][]

7.5 Анализ процесса с помощью контрольных карт

Цель анализа процесса можно определить так: выявление характерных случаев вариации показателей качества процесса. После выявления таких случаев в ходе анализа процесса надо провести серию действенных мер против них.

Разбиение на подгруппы – наиболее важная часть подготовки контрольной карты которая, определяет ее работоспособность. Неподходящий способ разбиения делает карту бесполезной.

После того как принято решение анализировать показатель качества процесса или управлять им, необходимо собрать данные. Вариация показателя качества процесса возникает по разным причинам. Соответственно до разбиения надо рассмотреть ту вариацию, которая требует исключения, а затем попытаться сгруппировать данные таким образом, чтобы вариация, обусловленная разрешенными факторами, образовала внутригрупповую вариацию. Для этой цели:

а) технологическую операцию следовало бы проводить при примерно одинаковых условиях (с технической точки зрения);

б) следует объединить в группы данные, собранные за относительно короткий период времени.

При группировании следует учитывать такие моменты:

а) существуют различные способы группирования. Вы должны выбрать объём подгруппы и испробовать различные способы комбинирования данных;

б) изменение способа группирования будет приводить к изменению тех факторов, которые образуют внутригрупповые вариации.

Нельзя эффективно применять контрольную карту, не зная компонентов внутригрупповой вариации. Следующий пример показывает, как меняется эта вариация в зависимости от способа группирования.

Пример. Размер детали используется как показатель качества процесса обработки. Главные факторы, влияющие на изучаемый размер, — это качество заготовок, форма резца и заточка затупления. Вот условия, в которых осуществляется данный процесс:

а) одной партии заготовок хватает на неделю работы;

б) резцы проверяются и затачиваются ежедневно;

в) резцы можно затачивать в начале утренней и вечерней смен.

В этом случае вариации качества между заточками рассматриваются как допустимые и критерий управления сводится к следующему: выполнена ли заточка достаточно правильно и обеспечивает ли резец нормальную работу. Тогда данные следует сгруппировать таким образом, чтобы вариация при одной заточке приводила к внутригрупповому разбросу, а вариация при разных заточках проявлялась в межгрупповом разбросе.

В таблице 7.6 приведены исходные данные, в таблице 7.7 и 7.8 показаны варианты группирования и, наконец, в таблице 7.9 представлены компоненты внутригрупповой и межгрупповой вариации соответственно.

1 Что такое контрольные карты?

Впервые контрольные карты были предложены в 1924 г. У. Шухартом с намерением исключить необычную вариацию: отделяя вариации, которые обусловлены определенными причинами, от тех, что обусловлены случайными причинами. Всякая контрольная карта состоит из центральной линии, пары контрольных пределов (по одному над и под центральной линией) и значений характеристики (показателя качества), нанесённых на карту для представления состояния процесса. Если все эти значения оказываются внутри контрольных пределов, не проявляя каких бы то ни было тенденций, то процесс рассматривается как находящийся в контролируемом состоянии. Если они попадут за контрольные пределы или примут какую — нибудь необычную форму, то процесс считается вышедшим из-под контроля. Примеры приведены на рисунке 7.1. Качество промышленной продукции в процессе производства неизбежно подвержено вариации. Для такой вариации есть различные причины, которые можно разделить на следующие два вида.

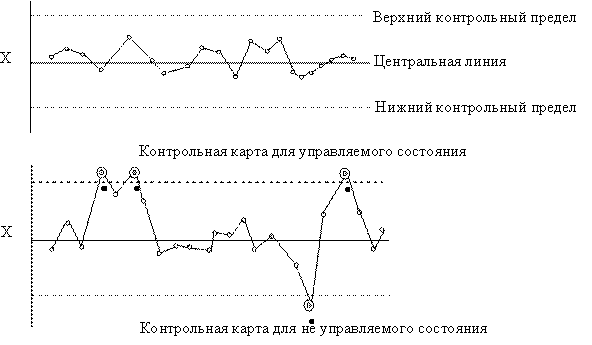Рисунок 7.1

Случайная причина. Вариация, обусловленная случайными причинами, необходима; она неизбежно встречается в любом процессе, даже если технологическая операция проводится с использованием стандартного сырья и традиционных методов. В настоящее время исключение случайных причин непрактично технически и экономически.

Определенная причина. Вариация, обусловленная определённой причиной, означает, что существуют факторы, допускающие изучение. Этих воздействий можно избежать и нельзя упускать такую возможность: бывают случаи, когда изменения вызваны несоблюдением стандартов или применением не тех стандартов.

Когда точки попадают за контрольные пределы или проявляют определённую тенденцию, мы говорим, что процесс вышел из–под контроля. Другими словами можно сказать, что существуют определённые причины вариаций, и процесс вышел из–под контроля. Чтобы управлять процессом, к этим причинам надо вернуться, хотя вариации, связанные со случайными причинами, допускаются.

Для построения контрольной карты необходимо оценить вариацию, обусловленную случайными причинами. Для этого мы делим данные на подгруппы, внутри которых остаются неизменными партия сырья, станок, оператор и другие общие факторы, так что вариации внутри подгрупп можно рассматривать примерно так же, как и вариации, обусловленные случайными причинами.

В зависимости от вида показателя и от цели существуют различные типы контрольных карт. В одном из типов контрольный предел вычисляется по такой формуле:

(среднее значение) ± 3 × (стандартное отклонение),

где стандартное отклонение и есть вариация, обусловленная случайными причинами. Этот тип контрольных карт называется контрольной картой с 3 – сигмовыми пределами.

7.3 Как построить контрольные карты

7.3.1 ( x -R) – карта

1. Соберите приблизительно 100 данных. Разделите их на 20 или 25 однородных подгрупп объёмом 4 или 5 в каждой. Заполните данными приготовленную таблицу (таблица 7.3). Когда практически нет повода для разделения данных на подгруппы, делите их в порядке поступления. В большинстве случаев объём группы берётся в интервале от 2 до 10.
2. Вычислите среднее x значение для каждой подгруппы:
   Гост р исо 7787-2-2012. инструменты стоматологические вращающиеся. фрезы. часть 2. карбидные лабораторные фрезы

   x =(х ₁ +х ₂ +х ₃ +х ₄ +…+х _n )/n,

   где n – объём подгрупп.

   Этот результат обычно подсчитывается с одним лишним десятичным знаком по сравнению с исходными данными.

3. Вычислите общее среднее значение X, деля итог столбца x для каждой из подгрупп на их число k:

   X = X ₁ + X ₂ +…+ X _k )/k,

   причём X надо вычислять с двумя лишними знаками по сравнению с измеренными значениями.

4. Вычислите размах R в каждой подгруппе, вычитая минимальное значение в подгруппе из максимального:

   R=(максимальное значение в подгруппе) – (минимальное значение в подгруппе).

   Таблица 7.3 Таблица данных для ( x -R ) – карты

5. Вычислите среднее значение R для размаха R, деля итог столбца размахов для всех подгрупп на их число k:

   R =(R ₁ +R ₂ +…+R _k )/k,

   Значение R надо вычислить с двумя лишними знаками по сравнению с измеренными значениями, т. е. с тем же числом знаков, что и X.

6. Вычислите каждую контрольную линию для x — карты и для R-карты по следующим формулам.

   x -карта. Центральная линия:

   CL= x

   Верхний контрольный предел:

   UCL= X +A ₂ R

   Нижний контрольный предел:

   LCL= x -A ₂ R

   R-карта. Центральная линия:

   CL= R

   Верхний контрольный предел:

   UCL=D ₄ R

   Нижний контрольный предел:

   LCL=D ₃ R

   Нижний предел не рассматривается, когда n меньше 6.

   Константы A ₂ , D ₄ , и D ₃ – коэффициенты, определяемые объёмом подгрупп (n), приведены в таблице 7.4.

   Таблица 7.4 – Перечень коэффициентов для ( x -R ) – карты

7. Нанесите слева вертикальную ось со значениями x и R и горизонтальные оси с номерами подгрупп. Разметьте верхний и нижний пределы так, чтобы между ними оказались 20 – 30 мм. Центральную линию сделайте сплошной, а контрольные пределы – пунктирными линиями.
8. Разметьте x и R для каждой подгруппы на одной и той же вертикальной оси напротив соответствующего номера подгруппы. Нанесите номера подгрупп на горизонтальную ось с интервалом в 2 – 5 мм. Чтобы легче было различать x и R, возьмём для x знак • (точка), для R — × (крестик), а для тех значений, которые выходят за пределы – кружочки.
9. Выпишите объём подгруппы (n) в верхнем левом углу x — карты. Запишите также и другие необходимые сведения, имеющие отношение к изучаемому процессу, такие как название процесса и продукта, период времени, метод измерения, условия работы, смена и т. д.

   Пример

   Так для первой группы:

   x =(47+32+44+35+20)/5=35,6

   X =(35,6+29,2+…+28,2)/25=29,86

   R=47-20=27

   R =27+18+…+27/25=27,44

   x — карта (рисунок 7.2)

   CL= X =29,86

   UCL= X =A ₂ R =29,86+0,577×27,44=45,69

   LCL= X -A ₂ R =29,86-0,577×27,44=14,03

   R-карта

   CL= R =27,44

   UCL=D ₄ R=2,115×27,44=58,04

   LCL=-(не рассматривается)

7.3.2 рn – карта

1. Возьмите выборку и классифицируйте продукцию по качеству на годную и бракованную в соответствии со стандартом. Теперь возьмите выборку такого объёма, чтобы в среднем в каждую подгруппу попадало от 1 до 5 негодных изделий и соберите 20 – 25 таких подгрупп (таблицу 7.5)

   Таблица 7.5 Таблица данных для pn – карты

2. Вычислите среднюю долю дефектов p, деля общее число дефектов в каждой подгруппе на общее число подгрупп:

   p =( Σ pn)/kn

3. Центральная линия:

   CL= p n

   Верхний контрольный предел:

   UCL= p n+3( p n(1- p )) ½

   Нижний контрольный предел:

   LCL= p n-3( p n(1- p )) ½

   Нижний предел не рассматривается, если его значение – отрицательное число.

4. Проведите горизонтальную ось с номерами подгрупп и вертикальную ось — с числами дефектов. Сплошной линией сделайте центральное значение p n и пунктирными линиями – верхний и нижний пределы. Затем нанесите на график числа дефектов для каждой подгруппы.

   Пример

   p =( Σ pn)/kn=68/(25×100)=0,0272

   CL= p n=0,0272×100=2,72 (рисунок 7.3)

   UCL= p n+3( p n(1- p )) ½ =2,72+3(2,72×(1-0,0272)) ½ =7,60

   LCL= p n-3( p n(1- p )) ½ =2,72-3(2,72×(1-0,0272)) ½ = (не рассматривается).

   pn — карта Рисунок 7.3

3.4. Метод обработки KUSUM-карт с использованием схемы интервалов принятия решений

В этом случае вводится две новые KUSUM-величины:

 ,                                                    
(79)

 ,                                                    
(80)

где  – некоторая
постоянная. Реализации величин (131)-(132)  и  сравниваются с
границами интервала принятия решений [, ].

При работе с такой контрольной картой действуют
следующим образом:

1.Пока
выполняются условия  и , контрольная карта не
заполняется.

2.Начиная
с  подсчитывается
сумма . Эта сумма уменьшается или
увеличивается в зависимости от величины ее новых слагаемых. Если она становится
меньшей или равной нулю, процесс счета прекращается.

3.Начиная
с  подсчитывается
сумма . Эта сумма уменьшается или
увеличивается в зависимости от величины ее новых слагаемых. Если она становится
большей или равной нулю, процесс счета прекращается.

4.После
прекращения счета образование  возобновляется, как только
выполнится , возобновление подсчета  начинается,
как только выполнится .

5.Если
 достигает
значения  или превышает его, то это
свидетельствует о том, что отклонение хода процесса от номинала  к
моменту времени , () настолько велико, что
необходимо предпринять вмешательство в процесс, уменьшая уровень настройки.

6.Если
 достигает
значения  или опускается ниже его, то это
свидетельствует о том, что отклонение хода процесса от номинала  к
моменту времени ,  () настолько велико, что
необходимо предпринять вмешательство в процесс, увеличивая уровень настройки.

Средняя линия такой контрольной карты ,
контрольные границы – горизонтальные линии на расстоянии  от средней.

При заданных вероятностях ошибок первого и
второго рода  параметры  определяется
соотношением

,                                                      
(81)

что справедливо, если
величины по оси абсцисс и оси ординат откладываются в тех же единицах. Если  единиц
(>0)
по оси ординат соответствует одной единице по оси абсцисс, то

.     
                                                    (82)

Для контрольных границ

.                                                    
(83)

[][]

Резюме

В заключение еще раз хочется подчеркнуть высокую эффективность применения контрольных карт в управлении качеством. Используя подходящие средства графического отображения, человеческий глаз способен отлавливать признаки ухудшения качества и тревожные тенденции в режиме поточного конвейерного производства.

При этом мощный аналитический пакет, такой как STATISTICA, способен взять на себе практически всю работу по обнаружению признаков разладки технологического процесса в online режиме, оставив оператору лишь анализ наиболее изощренных критериев визуальной проверки качества (малых трендов).

2.1. Коэффициенты устойчивости производственного процесса

Модифицированные карты Шухарта предназначены для
управления процессом по уровню настройки с учетом заданных полей допусков.

Если заданы поля допуска  и  для признака
качества ,  то на этапе пуска
производственного процесса необходимо оценить его устойчивость. Степень
устойчивости процесса зависит от того, насколько велика доля изделий, для
которых признак качества  находится в поле допуска [,]. На
практике об устойчивости процесса судят по коэффициенту устойчивости – безразмерной
величине, служащей мерой устойчивости производственного процесса.

Наиболее распространенной мерой устойчивости процесса
является неотрицательный коэффициент

 .                                                          
(25)

Например, требование  требует выполнения
условия .  Коэффициент  не зависит от
уровня настройки процесса. Его можно интерпретировать как меру потенциальной
устойчивости процесса.

Коэффициент

,                                                       
(26)

где

                                                        
(27)

и

                                                       (28)

 –
середина поля допуска, учитывает не только рассеяние, но и уровень настройки
процесса. Он характеризует различие между действительным и оптимальным уровнем
настройки процесса . Чем меньше , тем ближе
уровень настройки к оптимальному. Если  коэффициент  лежит между 0 и
.

            Следующий
коэффициент устойчивости

,                                                        (29)

где

.

Поэтому для коэффициента  можно использовать
выражение

.                            (30)

В то же время

.                                            
(31)

[][]

Контроль качества по атрибуту

Другим типом контрольных карт являются карты по атрибутивному признаку (атрибуту) – например, по числу дефектных деталей в партии, по числу отклонений характеристик изделия от стандарта в расчете на выборку.

Преимущество контрольных карт по атрибутивному признаку состоит в возможности быстро получить общее представление о различных аспектах качества анализируемого изделия; то есть, на основании различных критериев качества инженер может сразу принять или забраковать продукцию.

Контрольные карты по атрибутивному признаку иногда позволяют обойтись без применения дорогих точных приборов и требующих значительных затрат времени для измерительных процедур. Кроме того, этот тип контрольных карт более понятен менеджерам, которые не разбираются в тонкостях методов контроля качества. Таким образом, с помощью этих карт можно более убедительно продемонстрировать руководству наличие проблем с качеством изделий.

Однако, по сравнению с контрольными картами по атрибутивному признаку, карты для непрерывных переменных обладают большей чувствительностью. Благодаря этому, контрольные карты для непрерывных переменных могут указать на существование проблемы ухудшения качества, прежде чем в потоке продукции появятся настоящие бракованные изделия, выделяемые с помощью контрольной карты по атрибутивному признаку.

Контрольные карты для непрерывных переменных можно считать предвестниками проблем ухудшения качества, которые предупреждают об их наличии задолго до того, как в процессе производства резко возрастет доля бракованных изделий.

Для контроля качества продукции по атрибутивному признаку обычно используются следующие типы карт:

• С-карта
• U-карта
• Np-карта
• P-карта

При использовании С- и U-карт принимается предположение о том, что дефекты контролируемой характеристики продукции встречаются сравнительно редко и контрольные пределы для данных типов карт рассчитываются на основе свойств распределения Пуассона (распределения редких событий).

В свою очередь контрольные пределы для Np- и P-карт рассчитываются на основе биномиального распределения, а не распределения редких событий. Поэтому данный тип карт должен использоваться в том случае, когда обнаружение дефекта не является редким событием (например, происходит более чем у 5% проверенных единиц продукции).

При этом на С- и Np-картах отображается число дефектов (в партии, в день, на один станок), а на U- и P-картах отображается относительная частота дефектов, то есть отношение числа обнаруженных дефектов к числу проверенных единиц продукции.

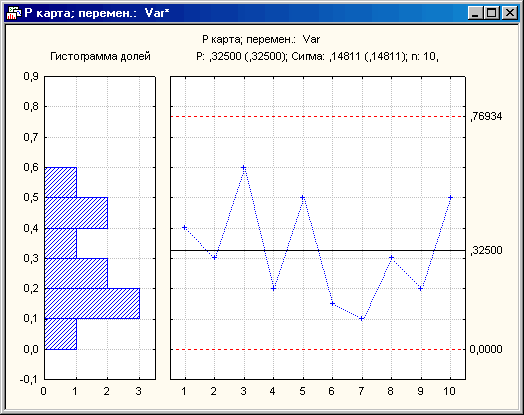
Рисунок 5

На рисунке выше представлен пример P-карты по атрибуту. На основе визуального анализа графика можно заключить, что данный процесс является управляемым: не наблюдается значений вне контрольных пределов (выбросов), нет заметного тренда, а также не наблюдаются систематические тенденции в расположении точек на карте.

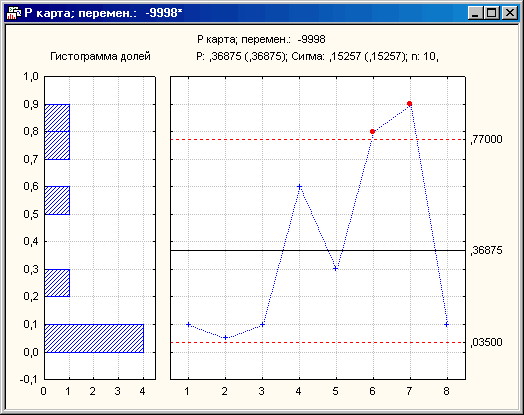
Рисунок 6

В противовес предыдущему графику на данной P-карте (см. Рисунок 6) демонстрируется «плохой» процесс. В шестой и седьмой выборках встречается более 80% бракованных изделий, что выше предопределенных контрольных пределов. Естественно такой высокий процент отбраковки продукции свидетельствует о наличии серьезных проблем качества данного производственного процесса.

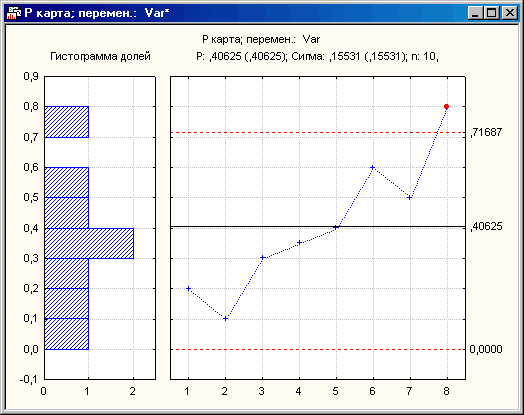
Рисунок 7

На следующей P-карте (см. Рисунок 7) также представлен пример «плохого» процесса. Причем, помимо выброса в последней выборке (80% брака), можно наблюдать систематическое увеличение процента бракованных изделий.

Аналогично продемонстрированным методам проводится визуальный анализ качества на основе других карт по атрибуту. Далее приводятся некоторые примеры текущего контроля качества на основе C-карты.

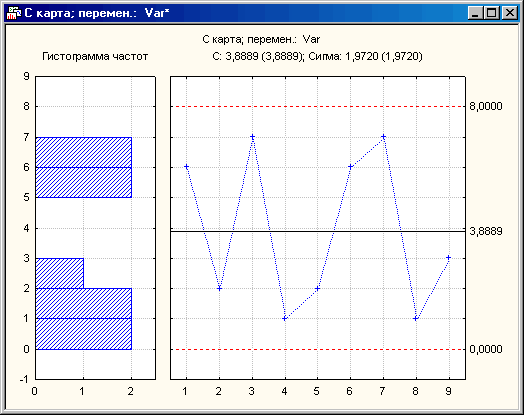
Рисунок 8

На этой С-карте показан хорошо управляемый технологический процесс: количество бракованной продукции в каждой выборке находится в рамках контрольных пределов.

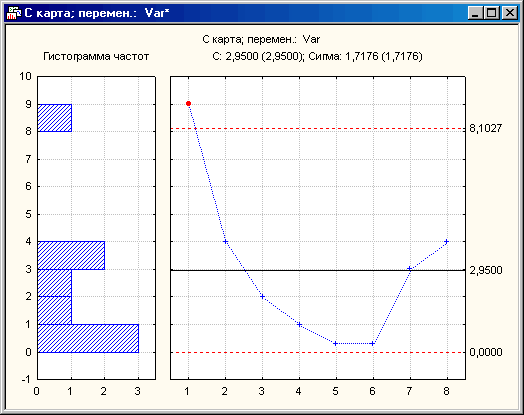
Рисунок 9

А в этом примере (см. Рисунок 9) на C-карте наблюдается выброс (первая выборка). Однако соответствующие статистики по остальным выборкам находятся в рамках контрольных пределов. Таким образом, на основании этой карты, исключив первую выборку, можно считать процесс управляемым. Если проблемная выборка отражает начало реального технологического процесса, то, скорее всего, ее неудовлетворительное качество связано с первоначальной настройкой процесса. В этом случае рекомендуется провести дополнительный анализ качества продукции, выпущенной на начальном этапе и, исключив имеющийся выброс, признать процесс управляемым.

Таблица 2. Квантили распределения размаха

n\w	0.001	0.005	0.01	0.025	0.05	0.1	0.3	0.5	0.7	0.9	0.95	0.975	0.99	0.995	0.999
2	0.00	0.01	0.02	0.04	0.09	0.18	0.54	0.95	1.47	2.33	2.77	3.17	3.64	3.97	4.65
3	0.06	0.13	0.19	0.30	0.43	0.62	1.14	1.59	2.09	2.90	3.31	3.68	4.12	4.42	5.06
4	0.20	0.34	0.43	0.59	0.76	0.98	1.53	1.98	2.47	3.24	3.63	3.98	4.40	4.69	5.31
5	0.37	0.55	0.67	0.85	1.03	1.26	1.82	2.26	2.73	3.48	3.86	4.20	4.60	4.89	5.48
6	0.53	0.75	0.87	1.07	1.25	1.49	2.04	2.47	2.94	3.66	4.03	4.36	4.76	5.03	5.62
7	0.69	0.92	1.05	1.25	1.44	1.68	2.22	2.65	3.10	3.81	4.17	4.49	4.88	5.15	5.73
8	0.83	1.08	1.20	1.41	1.60	1.84	2.38	2.79	3.24	3.93	4.29	4.60	4.99	5.25	5.82
9	0.97	1.21	1.34	1.55	1.74	1.97	2.51	2.92	3.35	4.04	4.39	4.70	5.08	5.34	5.90
10	1.08	1.33	1.47	1.67	1.86	2.09	2.62	3.02	3.46	4.03	4.47	4.78	5.16	5.42	5.97
11	1.19	1.45	1.58	1.78	1.97	2.20	2.72	3.12	3.55	4.21	4.55	4.86	5.23	5.49	6.04
12	1.29	1.55	1.68	1.88	2.07	2.30	2.82	3.21	3.63	4.28	4.62	4.92	5.29	5.55	6.09
13	1.39	1.64	1.77	1.98	2.16	2.39	2.90	3.28	3.70	4.35	4.68	4.99	5.35	5.60	6.14
14	1.47	1.72	1.86	2.06	2.24	2.47	2.97	3.36	3.77	4.41	4.74	5.04	5.40	5.65	6.19
15	1.55	1.80	1.93	2.14	2.32	2.54	3.04	3.42	3.83	4.47	4.8	5.09	5.45	5.70	6.23
16	1.62	1.88	2.01	2.21	2.39	2.61	3.11	3.48	3.89	4.52	4.85	5.14	5.49	5.74	6.27
17	1.69	1.94	2.07	2.27	2.45	2.67	3.17	3.54	3.94	4.57	4.89	5.18	5.54	5.78	6.31
18	1.76	2.01	2.14	2.34	2.52	2.73	3.22	3.59	3.99	4.61	4.93	5.22	5.57	5.82	6.35
19	1.82	2.07	2.20	2.39	2.57	2.79	3.27	3.64	4.03	4.65	4.97	5.26	5.61	5.86	6.38
20	1.88	2.13	2.25	2.45	2.63	2.84	3.32	3.69	4.08	4.69	5.01	5.30	5.65	5.89	6.41

Выход][

2.2. Определение контрольных границ

Пусть заданы два предельных значения  и .
Уровень средней линии  определяется серединой поля
допуска . Взятое из текущего процесса
изделие с показателем качества  бракуется как дефектное с
вероятностью

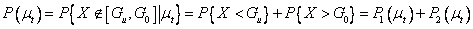.              (32)

В случае нормального закона показателя качества –

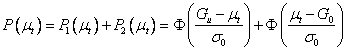.                         (33)

Минимальная доля брака согласно (85) получается при

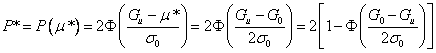.            (34)

При определении контрольных границ на контрольной
карте для управления процессом по уровню настройки с учетом заданных границ
поля допуска [,] исходят из того, что
уровень  настройки  процесса внутри поля
допуска может смещаться от его середины до уровня, при котором доля брака  достигает
некоторого критического значения . При достижении критического
значения  процесс останавливают на
поднастройку с заданной вероятностью . То есть, для используемой
контрольной статистики

.                                        (35)

При нормальности закона распределения рассматриваемой
статистики  показателя качества процесса при
вычислении контрольных границ можно полагать, что

,                                    (36)

.                                   
(37)

При значениях коэффициента  

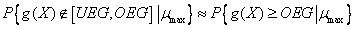,                    (38)

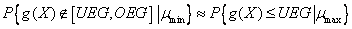.                    (39)

И с хорошим приближением можно считать

,                                           
(40)

.                                           
(41)

При этом  и  вычисляются как:

,                                                    
(42)

.                                                    
(43)

Так как контрольные границы по (92)-(93) должны лежать
внутри интервала [,] и в связи с
симметричностью одинаково удалены от  и , их можно представить в
виде:

,                                                     (44)

.                                                    
(45)

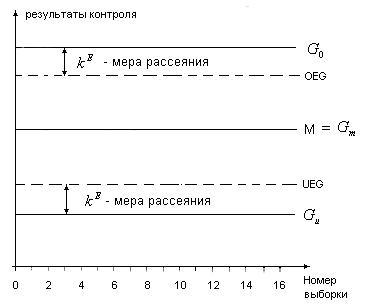
Рис.5. Схема двусторонней карты для управления
процессом по уровню настройки

[][]