Ост 34 10 616 93
Содержание:
Прайс-лист на опоры скользящие и неподвижные с направляющим хомутом ОСТ 34-10-620-93
| № | Наименование | Тип | Вертикальная нагрузка, кН | Диаметр Дн, мм | Ширина опоры, мм | Масса блоков, кг | Стоимость за ед. руб.* |
|---|---|---|---|---|---|---|---|
| 1 | 57У-01 ОСТ 34-10-620-93 | 1 | 1,0 | 57 | 74 | 0,20 | 140 р. |
| 2 | 57К-02 ОСТ 34-10-620-93 | 1 | 1,0 | 57 | 74 | 0,30 | 230 р. |
| 3 | 57У-03 ОСТ 34-10-620-93 | 2 | 1,0 | 57 | 74 | 0,23 | 140 р. |
| 4 | 57К-04 ОСТ 34-10-620-93 | 2 | 1,0 | 57 | 74 | 0,34 | 240 р. |
| 5 | 76У-05 ОСТ 34-10-620-93 | 1 | 1,0 | 76 | 92 | 0,23 | 140 р. |
| 6 | 76К-06 ОСТ 34-10-620-93 | 1 | 1,0 | 76 | 92 | 0,35 | 250 р. |
| 7 | 76У-07 ОСТ 34-10-620-93 | 2 | 1,0 | 76 | 92 | 0,26 | 140 р. |
| 8 | 76К-08 ОСТ 34-10-620-93 | 2 | 1,0 | 76 | 92 | 0,41 | 280 р. |
| 9 | 89У-09 ОСТ 34-10-620-93 | 1 | 1,0 | 89 | 108 | 0,35 | 150 р. |
| 10 | 89К-10 ОСТ 34-10-620-93 | 1 | 1,0 | 89 | 108 | 0,49 | 290 р. |
| 11 | 89У-11 ОСТ 34-10-620-93 | 2 | 1,0 | 89 | 108 | 0,38 | 150 р. |
| 12 | 89К-12 ОСТ 34-10-620-93 | 2 | 1,0 | 89 | 108 | 0,55 | 310 р. |
| 13 | 108У-13 ОСТ 34-10-620-93 | 1 | 1,5 | 108 | 128 | 0,40 | 150 р. |
| 14 | 108К-14 ОСТ 34-10-620-93 | 1 | 1,5 | 108 | 128 | 0,57 | 320 р. |
| 15 | 108У-15 ОСТ 34-10-620-93 | 2 | 1,5 | 108 | 128 | 0,45 | 150 р. |
| 16 | 108К-16 ОСТ 34-10-620-93 | 2 | 1,5 | 108 | 128 | 0,67 | 350 р. |
| 17 | 133У-17 ОСТ 34-10-620-93 | 1 | 2,5 | 133 | 156 | 0,87 | 180 р. |
| 18 | 133К-18 ОСТ 34-10-620-93 | 1 | 2,5 | 133 | 156 | 1,07 | 360 р. |
| 19 | 133У-19 ОСТ 34-10-620-93 | 2 | 2,5 | 133 | 156 | 0,92 | 180 р. |
| 20 | 133К-20 ОСТ 34-10-620-93 | 2 | 2,5 | 133 | 156 | 1,09 | 410 р. |
| 21 | 159У-21 ОСТ 34-10-620-93 | 1 | 2,5 | 159 | 182 | 1,00 | 190 р. |
| 22 | 159К-22 ОСТ 34-10-620-93 | 1 | 2,5 | 159 | 182 | 1,24 | 420 р. |
| 23 | 159У-23 ОСТ 34-10-620-93 | 2 | 2,5 | 159 | 182 | 1,07 | 190 р. |
| 24 | 159К-24 ОСТ 34-10-620-93 | 2 | 2,5 | 159 | 182 | 1,38 | 460 р. |
| 25 | 219У-25 ОСТ 34-10-620-93 | 1 | 5,0 | 219 | 246 | 2,13 | 280 р. |
| 26 | 219К-26 ОСТ 34-10-620-93 | 1 | 5,0 | 219 | 246 | 2,54 | 650 р. |
| 27 | 219У-27 ОСТ 34-10-620-93 | 2 | 5,0 | 219 | 246 | 2,27 | 300 р. |
| 28 | 219К-28 ОСТ 34-10-620-93 | 2 | 5,0 | 219 | 246 | 2,82 | 790 р. |
| 29 | 273У-29 ОСТ 34-10-620-93 | 1 | 7 | 273 | 300 | 2,36 | 310 р. |
| 30 | 273К-30 ОСТ 34-10-620-93 | 1 | 7 | 273 | 300 | 2,57 | 750 р. |
| 31 | 273У-31 ОСТ 34-10-620-93 | 2 | 7 | 273 | 300 | 2,50 | 330 р. |
| 32 | 273К-32 ОСТ 34-10-620-93 | 2 | 7 | 273 | 300 | 3,15 | 910 р. |
| 33 | 325У-33 ОСТ 34-10-620-93 | 1 | 14 | 325 | 352 | 3,32 | 440 р. |
| 34 | 325К-34 ОСТ 34-10-620-93 | 1 | 14 | 325 | 352 | 4,22 | 1 230 р. |
| 35 | 325У-35 ОСТ 34-10-620-93 | 2 | 14 | 325 | 352 | 3,79 | 500 р. |
| 36 | 325К-36 ОСТ 34-10-620-93 | 2 | 14 | 325 | 352 | 4,56 | 1 700 р. |
| 37 | 377У-37 ОСТ 34-10-620-93 | 1 | 20 | 377 | 406 | 3,66 | 480 р. |
| 38 | 377К-38 ОСТ 34-10-620-93 | 1 | 20 | 377 | 406 | 4,75 | 1 560 р. |
| 39 | 377У-39 ОСТ 34-10-620-93 | 2 | 20 | 377 | 406 | 4,13 | 540 р. |
| 40 | 377У-40 ОСТ 34-10-620-93 | 2 | 20 | 377 | 406 | 5,50 | 1 830 р. |
| 41 | 426У-41 ОСТ 34-10-620-93 | 1 | 25 | 426 | 450 | 6,00 | 780 р. |
| 42 | 426У-42 ОСТ 34-10-620-93 | 1 | 25 | 426 | 450 | 7,06 | 1 740 р. |
| 43 | 426У-43 ОСТ 34-10-620-93 | 2 | 25 | 426 | 450 | 7,00 | 910 р. |
| 44 | 426К-44 ОСТ 34-10-620-93 | 2 | 25 | 426 | 450 | 8,06 | 3 240 р. |
| 45 | 478У-45 ОСТ 34-10-620-93 | 1 | 30 | 478 | 510 | 6,80 | 890 р. |
| 46 | 478К-46 ОСТ 34-10-620-93 | 1 | 30 | 478 | 510 | 8,20 | 2 140 р. |
| 47 | 478У-47 ОСТ 34-10-620-93 | 2 | 30 | 478 | 510 | 8,00 | 1 040 р. |
| 48 | 478К-48 ОСТ 34-10-620-93 | 2 | 30 | 478 | 510 | 9,20 | 3 870 р. |
| 49 | 530У-49 ОСТ 34-10-620-93 | 1 | 40 | 530 | 560 | 7,25 | 950 р. |
| 50 | 530К-50 ОСТ 34-10-620-93 | 1 | 40 | 530 | 560 | 8,35 | 2 210 р. |
| 51 | 530У-51 ОСТ 34-10-620-93 | 2 | 40 | 530 | 560 | 8,65 | 1 080 р. |
| 52 | 530К-52 ОСТ 34-10-620-93 | 2 | 40 | 530 | 560 | 10,0 | 4 060 р. |
* — Цены указаны с учетом НДС. Цена может быть измена в зависимости от объема заказа и сроков изготовления.
ОСТ 34-42-676-84
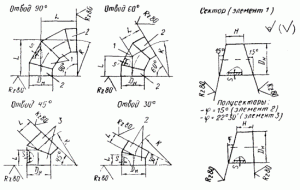
Детали и сборочные единицы трубопроводов АЭС Рраб<2,2 МПа (22 кгс/см2), Т<=350 °C. Тройники сварные переходные. Конструкция и размеры
| Обозначение: | ОСТ 34-42-676-84 |
| Обозначение англ: | OST 34-42-676-84 |
| Статус: | заменен |
| Название рус.: | Детали и сборочные единицы трубопроводов АЭС Рраб<2,2 МПа (22 кгс/см2), Т<=350 °C. Тройники сварные переходные. Конструкция и размеры |
| Дата добавления в базу: | 01.09.2013 |
| Дата актуализации: | 01.02.2020 |
| Дата введения: | 20.09.1984 |
| Дата окончания срока действия: | 24.02.2013 |
| Область применения: | Стандарт распространяется на тройники сварные переходные из углеродистой стали для трубопроводов второго контура атомных электростанций. |
| Разработан: | ПТИ Энергомонтажпроект Минэнерго СССР |
| Утверждён: | 24.04.1984 Министерство энергетики и электрификации СССР (USSR Ministry of Energy and Electrical Power 163) |
| Принят: | ВГНИПИИ Атомтеплоэлектропроект |
| Расположен в: |
Техническая документация Экология ЭНЕРГЕТИКА И ТЕПЛОТЕХНИКА Атомная энергетика Атомная энергетика, прочие аспекты ГИДРАВЛИЧЕСКИЕ И ПНЕВМАТИЧЕСКИЕ СИСТЕМЫ И КОМПОНЕНТЫ ОБЩЕГО НАЗНАЧЕНИЯ Трубопроводы и их компоненты Чугунные и стальные трубы |
| Чем заменён: |
|
| Нормативные ссылки: |
|












Отличия от ГОСТ 34.10-94 (старый стандарт) Править
Алгоритм формирования подписи отличается только в . В старом стандарте в этом пункте вычисляются $ \tilde{r}=a^k\pmod{p} $ и $ r=\tilde{r}\pmod{q} $ и если $ r=0 $, возвращаемся к пункту 3. Где $ 1<a<p-1 $ и $ a^q=1\pmod{q} $.
Алгоритм проверки подписи отличается только в . В старом стандарте в этом пункте вычисляется $ R = (a^{z1}y^{z2}\pmod{p})\pmod{q} $. Если $ R=r $, подпись правильная, иначе неправильная. Где $ y $ — открытый ключ для проверки подписи, $ y=a^d\pmod{p} $.
Здесь $ q $ — простое число, $ 2^{254}<q<2^{256} $ и $ q $ является делителем $ p-1 $.
Использование математического аппарата группы точек эллиптической кривой, позволяет существенно сократить порядок модуля $ p $, без потери криптостойкости.
Также старый стандарт описывает механизмы получения чисел $ p $, $ q $ и $ a $.
Алгоритм Править
Параметры схемы цифровой подписи Править
- точка $ P(x_P,\;y_P)\neq0 $ эллиптической кривой $ E $, являющаяся генератором подгруппы порядка $ q $, или другими словами $ qP=0 $. Здесь $ qP=P+P+… $($ q $ раз). А $ 0 $ — нулевой элемент группы точек эллиптической кривой.
Каждый пользователь цифровой подписи имеет личные ключи
- ключ шифрования $ d $ — целое число, лежащее в пределах $ 0<d<q $.
- ключ расшифрования $ Q(x_Q,\;y_Q) $ — точка эллиптической кривой, $ dP=Q $.
При этом должны выполняться
- $ p^t\neq 1 \pmod{q} $, $ \forall t=1..B $, где $ B\geq 31 $
- $ J(E)\neq 0 $ и $ J(E)\neq 1728 $
Двоичные векторы Править
Результатом операции конкатенации двух векторов $ \bar{h_1}=(\alpha_{255},…,\alpha_0) $ и $ \bar{h_2}=(\beta_{255},…,\beta_0) $ называется вектор длины 512 $ (\bar{h_1}|\bar{h_2})=(\alpha_{255},…,\alpha_0,\beta_{255},…,\beta_0) $.Обратная операция — операция разбиения одного вектора длины 512 на два вектора длины 256.
Формирование цифровой подписи Править
Forming of sign gost P34.10-2001.png
Формирование цифровой подписи
Checking of sign gost P34.10-2001.png
Проверка цифровой подписи
Добавить фото в галерею
- Вычисление хэш-функции от сообщения М: $ \bar{h} = h(M) $
- Вычисление $ e=z\pmod{q} $, и если $ e=0 $, положить $ e=1 $. Где $ z $ — целое число соответствующее $ \bar{h} $
- Генерация случайного числа $ k $, такого что $ 0<k<q $
- <span id=»forming4″ />Вычисление точки эллиптической кривой $ C=kP $, и по ней нахождение $ r=x_c\pmod{q} $ ($ x_c $ — координата $ x $ кривой $ C $). Если $ r=0 $, возвращаемся к предыдущему шагу.
- Нахождение $ s=rd+ke\pmod{q} $. Если $ s=0 $, возвращаемся к шагу 3.
- Формирование цифровой подписи $ \xi=(\bar{r}|\bar{s}) $, где $ \bar{r} $ и $ \bar{s} $ — векторы, соответствующие $ r $ и $ s $.
Проверка цифровой подписи Править
- Вычисление по цифровой подписи $ \xi $ чисел $ r $ и $ s $, учитывая, что $ \xi=(\bar{r}|\bar{s}) $, где $ r $ и $ s $ — числа, соответствующие векторам $ \bar{r} $ и $ \bar{s} $. Если хотя бы одно из неравенств $ r<q $ и $ s<q $ неверно, то подпись неправильная.
- Вычисление хэш-функции от сообщения М: $ \bar{h} = h(M) $
- Вычисление $ e=z\pmod{q} $, и если $ e=0 $, положить $ e=1 $. Где $ z $ — целое число соотвествующее $ \bar{h} $
- Вычисление $ \nu=e^{-1}\pmod{q} $.
- Вычисление $ z_1=s\nu\pmod{q} $ и $ z_2=-r\nu\pmod{q} $
- <span id=»verification6″ />Вычисление точки эллиптической кривой $ C=z_1P+z_2Q $. И определение $ R=x_c\pmod{q} $, где $ x_c $ — координата $ x $ кривой $ C $. В случае равенства $ R=r $ подпись правильная, иначе — неправильная.
Примечания
- (недоступная ссылка). bestpravo.ru. Дата обращения 1 сентября 2019.
- ↑ Игоничкина Е. В. . Дата обращения 16 ноября 2008.
- Семёнов Г. . «Открытые системы» № 7-8/2002 (8 августа 2002). Дата обращения 16 ноября 2008.
- Бондаренко М. Ф., Горбенко И. Д., Качко Е. Г., Свинарев А. В., Григоренко Т. А. . Дата обращения 16 ноября 2008.
-
Leontiev, S., Ed. and G. Chudov, Ed. (англ.) (декабрь 2008). — Internet-Drafts, work in progress. Дата обращения 12 июня 2009.
-
S. Leontiev, P. Smirnov, A. Chelpanov. (англ.) (декабрь 2008). — Internet-Drafts, work in progress. Дата обращения 12 июня 2009.
-
V. Dolmatov, Ed. (англ.) (апрель 2009). — Internet-Drafts, work in progress. Дата обращения 12 июня 2009.